State pigeonhole principle. Solve the recurrence relation a_n = 3a_n-1 –  3a_n-2 + a_n-3 with initial conditions a₀=1 ,a₁ = 3, a₂=7.

Find the value of x such that x = 1 (mod 3), x = 1 (mod 4),  x = 1 (mod 5) and x = 0 (mod 7) using Chinese remainder theorem.

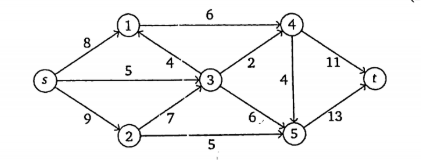
Define Euler circuit with suitable example. Find the maximal flow s to t from the given network flow.

Prove that for every positive integer n ≥ 1, n²+n is even integer using mathematical induction.

All over smart people are stupid. Children of stupid people are naughty. John is a children of Jane. Jane is over smart. Represent these statements in FOPL and prove that John is naughty.

Which of the following are possets?

1. (Z, =)
2. (Z, ≠)
3. (Z, ⊆)

Define reflexive closure and symmetric closure. Find the remainder when 4x² – x + 3  is divided by x + 2 using remainder theorem.

Define Euler path and Hamilton path. Give examples of both Euler and Hamilton path.

How many 3 digits numbers can be formed from the digits 1,2,3,4 and 5 assuming that:

1. Repetitions of digits are allowed
2. Repetitions of digits are not allowed

What is minimum spanning tree? Explain Kruskal’s algorithm for finding minimum spanning tree.

List any two applications of graph coloring theorem. Prove that “A tree with n vertices has n-1 edges”

Define ceiling and floor function. Why do we need Inclusion – Exclusion principle? Make it clear with suitable example.